Integral Teknik Integral Parsial

Teknik Integral Parsial

by Reziono Pratama in Integral

Teknik pengintegralan parsial didasarkan pada pengintegralan rumus turunan hasil kali dua fungsi.

Teorema 3

Jika u = u(x) dan v = v(x) masing-masing fungsi terdiferensial, maka 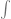$\int$ u dv = uv – 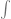$\int$ v du.

Bukti :

Dari rumus turunan hasil kali dua fungsi diperoleh

$\dfrac{d}{dx}$ (uv) = ( $\dfrac{d}{dx}$ u(x)) v(x) + ( $\dfrac{d}{dx}$ v(x)) u(x)

= v $\dfrac{du}{dx}$ + u $\dfrac{dv}{dx}$

Pengintegralan pada kedua ruas menghasilkan

$\int$ ( $\dfrac{d}{dx}$ (uv))dx = $\int$ (v $\dfrac{du}{dx}$ ) + $\int$ (u $\dfrac{dv}{dx}$ )

$\Leftrightarrow$ uv = $\int$ v du + $\int$ u dv

$\Leftrightarrow$ u dv = uv + $\int$ v du $\blacksquare$

Contoh :

$\int$ xe-x dx = …

ambil u = x dan dv = e-x dx $\Leftrightarrow$ v = -e-x, maka

$\int$ xe-x dx = $\int$ u dv = uv – $\int$ v du

= -xe-x – $\int$ e-x dx

= -xe-x – e-x + C

Atau bisa juga dikerjakan seperti ini

$\int$ xe-x dx = $\int$ x d $\dfrac{e^{-x}}{-e^{-x}}$

= – $\int$ x d(e-x)

= -(xe-x – $\int$ e-x dx)

= -(xe-x + e-x) + C

= -xe-x + e-x + C
$\int$ ex sin x dx = …

$\int$ ex sin x dx = $\int$ sin x d(ex)

= ex sin x – $\int$ ex d(sin x)

= ex sin x – $\int$ ex cos x dx

= ex sin x – $\int$ cos x d(ex)

= ex sin x – [ex cos x – $\int$ ex d(cos x)]

= ex sin x – [ex cos x – $\int$ – ex sin x]

= ex sin x – ex cos x – $\int$ ex sin x dx

sehingga diperoleh,

= 2 $\int$ ex sin x dx

= ex sin x – ex cos x

$\Leftrightarrow$ $\int$ ex sin x dx = $\dfrac{1}{2}$ (ex sin x – ex cos x) + C
$\int$ ln x dx = …

$\int$ ln x dx = x ln x – $\int$ x d(ln x)

= x ln x – $\int$ x $\dfrac{1}{x}$ dx

= x ln x – $\int$ dx

= x ln x – x + C
$\int$ x $\sqrt{x+3}$ dx = …

$latex \int$ x $\sqrt{x+3}$ dx = $\int$ x $\dfrac{2}{3}$ d(x + 3)3/2

= $\dfrac{2}{3} \int$ x d(x + 3)3/2

= $\dfrac{2}{3}$ [x(x + 3)3/2 – $\int$ (x + 3)3/2 dx]

= $\dfrac{2}{3}$ [x(x + 3)3/2 – $\int$ (x + 3)3/2 d(x + 3)]

= $\dfrac{2}{3}$ [x(x + 3)3/2 – $\dfrac{2}{5}$ (x + 3)3/2] + C

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

Copy Right 2017 by SeoHub